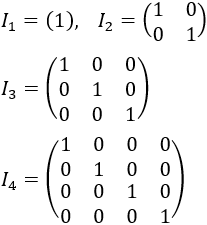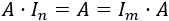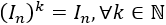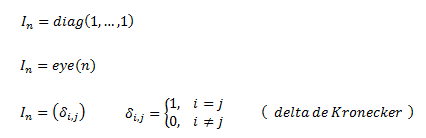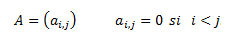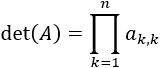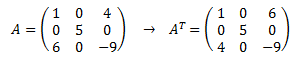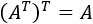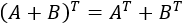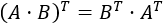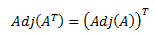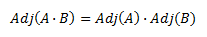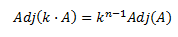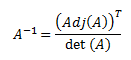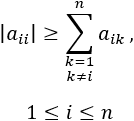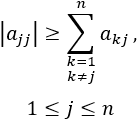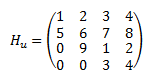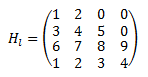Solución sistema ecuaciones método de Gauss-Jordan

PLANTEAMIENTO DEL PROBLEMA

 Primer punto: Plantear el sistema de ecuaciones para hallar un número de tres cifras sabiendo que la suma de sus cifras es 11, que la suma de la primera y la tercera cifra es 5 y que la segunda cifra es el doble de la tercera.

X=0

Y=0

Z=0

X+Y+Z=11

X+Z=5

Y=2Z

Sustituimos en la primera ecuación y que es igual a 2Z.

X+2Z+Z=11 à

X+3Z=11

X+Z=5

Y=2Z

Me quedan las dos primeras ecuaciones con dos incógnitas:

Resuelvo estas por reducción, realizando la resta:

      X+3Z=11

 -     X+Z=5

__________________

     2Z=6    --àZ=3

Reemplazo Z en la tercera ecuación:

Y=2(3)à Y= 6

Reemplazo Z en la primera ecuación y hallamos X.

            X+2(3)+3=11àX=2

X= 2, Y= 6 , Z= 3

Entonces el numero es 2 6 3.

Segundo punto:  Resolver el siguiente sistema de ecuaciones por el método de Gauss

 x  + 2y - 3z = -16

3x +  y  - 2z = -10

 2x - 3y +  z  = -4

Hacemos la matriz aumentada:

  X     Y       Z

  1     2      -3     -16

  3    1       -2     -10

  2    -3       1     -4

La celda (2, 1) la convertimos en cero, entonces F2* 3 -F3*2

  1     2      -3     -16

  0    11     -7     -22

  2    -3       1     -4

La celda (3,1) la convierto en cero, entonces 2F1-F3

  1     2      -3     -16

  0    11     -7     -22

  0      7      -7    -28

Dividimos la F3 entre 7

  1     2      -3     -16

  0    11     -7     -22

  0      1      -1    -4

Encontramos el cero en la celda (3,2) entonces 11F3-F2

  1     2      -3     -16

  0    11     -7     -22

  0      0     -4    -22

_4z=-22->Z =-22/-4àZ=5.5

11Y-7(5.5)=-22->y= 11Y -38.5=-22àY= 16.5/11àY=1.5

X+2(1.5)+(-3)(5.5)=-16àx+3-16.5=-16àX=13.5-16àX=-2.5

x  + 2y - 3z = -16 à 5.5+3+7.5=-16à16=16

Tercer Punto Resolver el siguiente sistema de ecuaciones lineales

 x +  y +  z  =  3  

      2y + 3z = 15

2x + 4y +5z =  21

a:  Y= -x-z+3

Sustituyo el valor de Y de la primera ecuación en la segunda ecuación.

2(x-z+3)+3z=15

2x-2z+6+3z=15à2x+z=9

Reemplazo Y en la tercera ecuación:

2x+4(-x-z+3)+5z=21à2x-4x-4z+12+5z=21à

-2x+z=9

  - 2x+z=9 despejamos z à

 z=9+2x y reemplazo en la siguiente ecuación

   6x+9+2x=9à 8x=0à x=0/4--àX=0

Reemplazo x en la anterior del valor de Z

z=9-2x

Z=9-2(0)-àz=9

Tenemos el valor z y el valor x lo reemplazamos en la primera en que despejamos Y ósea en a.

Y=9-0+3-ày=12

x +  y +  z  =  3  -à 0+12+3=12

Reemplazamos en cualquier ecuación para comprobar la igualdad:

­­­­­­­­­­­­­­­­­­­­­­­

Utilizo el método de determinantes o regla de Cramer:

  1     1      1      3    Repetimos debajo de  tercera fila las 2 primeras

  0     2       3    15

 2      4      5    21

 1       1      1    3

  0     2       3     15

(1* 2 * 5+ 0*4*1+ 2*1 *3)-(1*2*2+3*4*1+5*1*0)

(10+0+6)-(4+12+0)= 16-16 =0  El determinante del sistema es cero ∆s=0

Buscamos el determinante de X y en la columna de X colocamos los términos independientes.

 3       1      1    1       1

15     2      3    15     2

  21      4     5    21    4

  (30+63+60)-(75+12+42)= 153-129= 24

∆x=24

Buscamos el determinante de Y, en la columna de Y colocamos los términos independientes.

  1     3        1         

  0     15       3   

2      21      5  

  1       3      1  

  0     15      3    

(75+21+18)-(30+63+15)=114-108= 6

∆Y=6

Buscamos el determinante de Z, en la columna de Z colocamos los términos independientes.

  1       1      3     1       1

 0       2      15    0      2

  2      4        21   2     4

(42+30+0)-(0+60+12)= 72-72 =0

∆Z=0

Tenemos: ∆x/∆s= 24/0=0

                  ∆y/∆s=  6/0=0

                  ∆z/∆s= 0/0=0

              El sistema no tiene solución

La diferencia es que, en la eliminación Gaussiana, se hacen ceros debajo de la diagonal principal, y entonces queda la última incógnita que se despeja inmediatamente, después se va a la penúltima ecuación que ha quedado y se despeja la penúltima incógnita y así sucesivamente.

El método de Gauss-Jordán continúa haciendo operaciones de suma de filas haciendo que por encima de la diagonal principal también haya ceros con lo cual queda una matriz diagonal y las incógnitas se despejan sin más que hacer una división. Yo prefiero el método primero, es muy pesado ir escribiendo la matriz tantas veces y en esta página aún más.

La ventaja de utilizar Gauss Jordán es que transforma la matriz de coeficientes en una matriz triangular superior. El método de Gauss-Jordán continúa el proceso de transformación hasta obtener una matriz diagonal unitaria (aij=0 para cualquier i diferente de J ).

!Muy importante! Para tener en cuenta:

Muestre la matriz ampliada original de cada sistema de ecuaciones en cada uno de los puntos. Indique las operaciones elementales y cada matriz resultante después aplicar cada paso. En cada punto debe hacer una reflexión si el sistema tiene solución, si es única y                en caso de no tenerla, por qué no la tiene. Si requiere de más espacio para el desarrollo puede agregar páginas necesarias 

Aplicación del álgebra matricial para la solución de sistemas de ecuaciones lineales

 Aplicación del álgebra matricial para la solución de sistemas de ecuaciones lineales

Solucion de sistemas de ecuaciones lineales usando matrices

resumen sobre los diferentes métodos que se aplican para solucionar sistemas de ecuaciones utilizando las matrices

Definiciones:

Una matriz de orden mxn es un arreglo rectangular de mn elementos dispuestos en m filas y n columnas.

Matriz transpuesta es la matriz que se le intercambian las filas for las columnas siendo T(aij) = bij = aji

Matriz simétrica es la matriz que su transpuesta es igual a la original, y antisimétrica es la matriz que su transpuesta es igual a la original con signo negativo.

Las matrices diagonales y triangulares juegan un papel importante en la descomposición de matrices que sustentan los algoritmos mas importantes del algebra lineal.

La diagonal principal de la matriz está conformada por aquellas entradas donde los subíndices son iguales i =j.

(i) Filas (j) Columnas

Una matriz es diagonal si y solo si todas las entradas de la diagonal son diferentes de cero y el resto son ceros.

Una matriz es triangular superior si y solo si todas las entradas donde los subíndices son i>j son cero.

Una matriz es triangular inferior si y solo si todas las entradas donde los subíndices son i<j son cero.

Un sistema de m ecuaciones lineales con n incognitas AX = b es soluble si existe al menos un vector S de n componentes constantes tal que AS = b. A un sistema que carece de solución lo llamamos no soluble o inconsistente.

Hay operaciones elementales de fila.

1. Sustraer a una fila un múltiplo de otra

2. Intercambiar dos filas

3. Multiplicar una fila por una constante diferente de cero

Método de Gauss-Jordan

Es un algoritmo para eterminar simultaneamente si una matriz cuadrada A tiene inversa y también resolver el sistema de ecuaciones.

Determinante

El determinante es una propiedad de las matrices que se obtiene realizando diferentes algoritmos. Esta propiedad contiene información obre la matriz y la solubilidad del sistema de ecuaciones

Regla de Cramer.

Es un método que usa determinantes para hallar la solución al sistema de ecuaciones.

Responder a las siguientes preguntas:

a. ¿Cual de los métodos es el más indicado para resolver un sistema de cuatro ecuaciones con cuatro incógnitas y por qué?

sin lugar a dudas el método de Gauss-Jordan es más eficiente computacionalmente.

b. ¿Que ventaja tiene resolver un sistema de ecuaciones dos por dos con el método de determinantes?

Los métodos con determinante para solucionar sistemas de ecuaciones previenen de realizar cálculos en exceso ya que el determinante del sistema no puede ser cero. ya que para usar la regla de Crammer la matriz debe necesariamente ser invertible.

c. Enumere al menos tres métodos para calcular un determinante.

Método de cofactores: consiste en escoger una fila o una columna, para cada término de la fila o columna, llamados cofactores, quitamos la fila o columna en la que está y lo que queda es el menor.

Después, multiplicar el valor del menor por el cofactor y por su signo y sumar lo de todos los cofactores

El determinante de una matriz de orden n se puede calcular de n^2 maneras diferentes ya que el desarrollo por cofactores se puede realizar por filas o por columnas.

Método de Sarrus: también llamado la estrella de David consiste en 2 partes, la primera es sumar la multiplicación de la diagonal, más la multiplicación del primer triángulo formado a la derecha de este y su inverso, a esto se le resta la multiplicación de la diagonal secundaria más el triángulo formado a su derecha más su inverso

Método único para matrices de 3x3: Este método consiste en aumentar a la derecha las dos primeras columnas o abajo las dos primeras filas de tal manera que con estas obtengamos la multiplicación de las diagonales principales y sumar sus productos de cada una y restar de este valor la suma de las multiplicaciones de las otras diagonales.

Matrices Especiales

 

Introducción

La importancia de las matrices en álgebra es conocida y existen numerosos teoremas que las caracterizan o que las emplean como herramienta. Pero además, si trabajamos con matrices especiales, esto es, con matrices que cumplen determinadas características, obtenemos otros resultados interesantes o importantes por sus aplicaciones. Veamos un ejemplo:
Dada la matriz regular A de dimensión n x n tiene todos los menores principales no singulares, entonces admite una factorización LU. En este caso, para resolver computacionalmente el sistema
$$Ax=b$$se necesitan
$$\frac{2}{3}{n}^3$$operaciones en punto flotante, mientras que si usamos la descomposición QR se necesitan
$$\frac{4}{3}{n}^3$$Es decir, usando la descomposición LU se requiere la mitad de operaciones respecto la descomposición QR.
En esta sección presentamos los tipos básicos de matrices según su forma (definición y propiedades inmediatas): identidad, diagonal, traspuesta, adjunta, simétrica, antisimétrica, definida positiva, diagonalmente dominante y Hessenberg.

Matriz identidad

Llamamos matriz identidad a la matriz cuadrada (mismo número de filas que de columnas) formada por unos en la diagonal y ceros en las demás entradas (posiciones). La representamos por In donde n es la dimensión de la matriz.

Propiedades:

• Es el neutro del producto de matrices. Es decir, para toda matriz A de dimensión m x n,
  
  
• Es idempotente, es decir, sus potencias son ella misma
  
  
• Es regular y su inversa es ella misma.
• Es una matriz permutación.
• Sólo tiene un autovalor (valor propio), que es 1, con multiplicidad algebraica la misma que la dimensión de la matriz.

Notaciones habituales:

Matriz diagonal

Todos los elementos son nulos excepto los de la diagonal, esto es, los elementos que tienen el mismo número de fila que de columna.
Una matriz A diagonal de dimensión m x n que tiene por elementos de la diagonal a los elementos del vector v se le denota por

Ejemplos

Propiedades:

• Son un caso particular de las matrices triangulares.
• La matriz traspuesta de una matriz diagonal de dimensión m x n es la matriz diagonal de dimensión n x m con la misma diagonal.
• En las matrices cuadradas, el determinante es el producto de los elementos de la diagonal:
  
  
  con lo que son regulares si, y sólo si, todos los elementos de la diagonal son distintos de 0. En tal caso,
  
  
• Potencias (para las cuadradas)
  
  
• Producto de matrices diagonales: Sean las matrices A y B diagonales de dimensiones respectivas m x n y n x t, su producto es una matriz diagonal de dimensión m x t
  
  
• Los autovalores (valores propios) de las matrices diagonales cuadradas son los elementos de la diagonal.

Matrices triangulares

Distinguimos dos tipos:

• triangular superior: todos los elementos por debajo de la diagonal de la matriz son 0, es decir,
  
  
• triangular inferior: todos los elementos por arriba de la diagonal de la matriz son 0, es decir,
  
  

Ejemplos
Triangular superior	Triangular inferior

Propiedades de las matrices triangulares

• La matriz traspuesta de una triangular superior es triangular inferior y viceversa.
• Si la matriz es cuadrada, su determinante es el producto de los elementos de la diagonal
  
  
  Por tanto, es regular si, y sólo si, los elementos de la diagonal son distintos de 0. En tal caso,
  
  
• La inversa de una matriz triangular superior (inferior) es una matriz triangular superior (inferior).
• El producto de matrices triangulares superiores (inferiores) es una matriz triangular superior (inferior).
• Los autovalores (valores propios) de una matriz cuadrada triangular son los elementos de la diagonal.

Matriz traspuesta

La matriz traspuesta de una matriz A de dimensión m x n es una matriz de dimensión n x m que tiene por columnas a las filas de A. Se denota como AT (o A' si la matriz es real).

Ejemplos

Propiedades de la matriz traspuesta

• Traspuesta de la traspuesta
  
  
• Traspuesta de la suma
  
  
• Traspuesta del producto
  
  
• Una matriz es igual que su traspuesta si, y sólo si, es simétrica
  
  
• El determinante de una matriz regular es igual al de su traspuesta
  
  

Matriz adjunta

Sea A una matriz de cuadrada de dimensión n

se define su matriz adjunta como

donde Ai , j es la matriz que resulta al quitar la fila i y columna j a A.
Al elemento ad i , j se le denomina ( i , j )- cofactor (o adjunto) de la matriz A.
Propiedades de la matriz adjunta:

• Adjunta de la identidad
  
  
• Adjunta de la traspuesta
  
  
• Adjunta del producto
  
  
• Si A es de dimensión n y k un escalar
  
  
• Si A es regular, su inversa es
  
  
  Esta propiedad se usa con frecuencia para el cálculo de la inversa: ejemplos.

Ejemplo de matriz adjunta

Matriz simétrica

Una matriz A cuadrada es simétrica si es igual a su traspuesta. Es decir,

Ejemplo

Propiedades de las matrices simétricas

• La inversa de una matriz simétrica regular es simétrica.
• La adjunta de una simétrica es simétrica.
• La suma de simétricas es simétrica. El producto lo es si, y sólo si, también es conmutativo.
• Los autovalores (valores propios) de una matriz cuadrada, real y simétrica son reales.
• Autovectores (vectores propios) de autovalores distintos de una matriz cuadrada y real son ortogonales.
• Una matriz cuadrada y real, A, es simétrica si, y sólo si, es diagonalizablemediante una matriz de paso ortogonal, Q. Es decir,
  
  

Matriz antisimétrica

Una matriz cuadrada A es antisimétrica si su traspuesta es igual a su opuesta, es decir, AT = -A.

Matriz definida positiva

Una matriz A de dimensión m x n es definida positiva si para todo vector x = ( x1 ,…, xn) se cumple

Si la desigualdad se cumple con el signo ≥ , diremos que es semi definida positiva.

Matriz (estrictamente) diagonalmente dominante por filas o columnas

Una matriz A de dimensión m x n es diagonalmente dominante por filas si

diremos que los es por columnas si

Diremos que los son estrictamente si la desigualdad se cumple de forma estricta: >.

Matriz Hessenberg

Una matriz cuadrada A de dimensión n > 1 diremos que es Hessenberg superior si todos los elementos por debajo de la diagonal -1 son nulos. Recordamos que la diagonal -k es la diagonal número k por debajo de la diagonal (principal).
Una matriz cuadrada A de dimensión n > 1 diremos que es Hessenberg inferior si todos los elementos por arriba de la diagonal -1 son nulos. Recordemos que la diagonal k es la diagonal número k por arriba de la diagonal (principal).

Ejemplos
Hessenberg superior
Hessenberg inferior